Par Bernard DÜRR •
ÉCHELLE : terme désignant l’ordre successif des sons dans un système mélodique donné, sans l’idée de tonique, d’organisation hiérarchisée ou de délimitation de tessiture. L’échelle ne doit pas être confondue avec le mode.
Sciences de la Musique Marc Honegger
Ou bien encore : une échelle musicale est une série de fréquences — sons ou hauteurs, habituellement appelées degrés — fixées par un système musical donné. Les sons dont il s’agit sont bien évidemment les sons harmoniques ou toniques , c’est à dire ceux dont la hauteur est perceptible. A priori tous les sons dont on peut percevoir la hauteur sont utilisables pour élaborer une mélodie. Une Echelle musicale opère une sélection sur cet ensemble en privilégiant des intervalles.
Un petit résumé historique
Il est convenu aujourd’hui de considérer que notre musique occidentale prend ses sources dans la musique grecque codifiée au quatrième siècle avant JC. Les premières échelles musicales nous ont été transmises par les philosophes et mathématiciens grecs qui ont trouvé dans la musique une source d’inspiration et un terrain expérimental, Pythagore et ses disciples, Archytas de Tarente, Aristoxène…
Échelles de hauteurs ou échelles d’intervalles
Les intervalles harmoniques
L’intervalle est le rapport entre deux hauteurs, deux fréquences, deux notes. Les superpositions d’ intervalles sont les accords. Les séquences d’intervalles sont des mélodies. Les grecs ont formalisé les premières échelles musicales de notre culture occidentale en identifiant sous forme de fraction les intervalles leur permettant de composer dans des modes particuliers, soit par leur couleur soit par leur origine géographique.
L’octave : 2, c’est le rapport entre la fréquence du second mode de vibration de la corde et la fréquence fondamentale. Ce rapport est celui de la similarité, deux notes séparées par un octave semblent être les mêmes.(Il semble que ce soit dû au mode de synchronisation des cellules ciliées- cf C.H.Chouard)
La quinte : 3/2 , c’est le rapport entre la fréquence du mode 3 et la fréquence du mode 2
La quarte : 4/3 , c’est le rapport entre la fréquence du mode 4 et la fréquence du mode 3
1 octave = 1 quinte + 1 quarte (3/2 x 4/3 = 2 )
Ces premiers intervalles sont de la forme (n+1)/n qui est le rapport entre deux fréquences consécutives de la série harmonique. On les appelle épimore ou super partiels.
Ce sont les intervalles les plus consonants.
La consonance est couramment attribuée à la fusion des harmoniques communs à deux sons selon l’intervalle représenté par le rapport de leurs fréquences fondamentales respectives. Pour un intervalle de la forme (n+1)/n (épimore), un harmonique sur (n+1) fusionne. Exemple:
- n=1, (n+1)/n = 2, 1 harmonique sur 2 fusionne pour l’octave
- n=2, (n+1)/n = 3/2, 1 harmonique sur 3 fusionne pour la quinte
- n= 3 (n+1)/n =4/3 1 intervalle sur 4 fusionne pour la quarte et c’est ainsi au fur et à mesure que n croit, la fusion diminue.
La perception de la consonance n’est pas si simple, la fusion n’explique pas tout. Les neurosciences nous disent que nos perceptions sont influencées par la motivation, l’hédonie ou le plaisir ressenti et l’apprentissage. La physique et les mathématiques n’expliquent pas la musique, elles permettent d’identifier les objets et les relations entre objets perçus mais pas les relations que nous avons avec ces objets. Celles-ci dépendent de notre « umwelt », notre monde propre à l’instant donné. La dissonance ne commence pas là où s’arrête la consonance. A propos de harmoniques éloignés Schoenberg écrit : « Ainsi que l’explique le calcul des oscillations, ils sont aussi peu antagonistes que ne le sont deux et dix, et les expressions de consonance et de dissonance qui tendent à signifier un antagonisme se révèlent dès lors fausses. Tout dépend seulement de la faculté croissante de l’oreille analytique de se familiariser avec les harmoniques lointains et d’élargir ainsi dans sa potentialité artistique, le concept de consonance afin qu’y trouve place un jour la totalité du phénomène sonore donné par la nature. » (in Traité d’Harmonie , Arnold Schoenberg 1911)
Les deux premiers intervalles épimores, la quinte et la quarte, ont indéniablement une fonction particulière que l’on retrouve dans les cadences de l’harmonie tonale.
Et entre la quinte et la quarte quel est l’intervalle? 3/2 divisé par 4/3, on multiplie le numérateur de la première fraction par le dénominateur de la seconde et inversement pour obtenir 9/8, le rapport entre la fréquence du mode 9 et celle du mode 8 :
1 quarte + 9/8 = 1 quinte, et alors
1 quarte + 9/8 + 1 quarte = 1 octave
On obtient la structure de base du tétracorde grec. Deux lyres de quatre cordes avec un intervalle de quarte entre la première et la dernière corde. Un intervalle appelé ton disjonctif entre la dernière corde du premier tétracorde et la première corde du second, on a ainsi 8 notes dans une octave, pourquoi pas appeler ça la gamme diatonique et les baptiser Do, ré, mi…mais ça viendra plus tard.
Entre les deux cordes extrêmes de chaque tétracorde les hauteurs n’étaient pas figées. Le musicien/compositeur pouvait régler la tension des cordes en fonction de l’humeur de sa composition ou d’un mode privilégié.
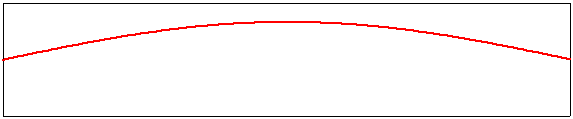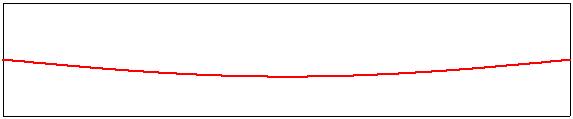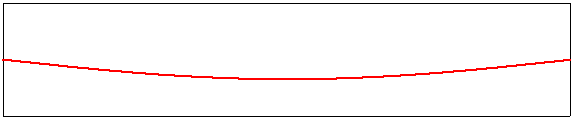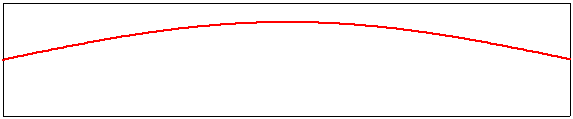
Corde vibrante : le mode fondamental
L’image ci-dessus illustre le premier mode de vibration d’une corde, maintenue par une extrémité fixe et une extrémité mobile. Il faut supposer qu’à l’une des extrémité s’exerce une tension fixe comme pour une corde de guitare par exemple. Dans ce mode appelé mode fondamental , on voit se former un arc dont la courbure varie, de façon continue, d’un maximum à un minimum et inversement. La corde vibre. Lorsque la longueur de la corde diminue, cette vibration se fait plus rapide. La fréquence de la vibration (qui ne correspond pas à celle de l’image qui est au ralenti) est affichée en Hertz(Hz).Une fréquence de 1 hertz correspond à une vibration complète par seconde. On associe à la hauteur d’un son la fréquence de son mode de vibration fondamentale. La fréquence de départ affichée, 220Hz, correspond à la hauteur de la note La2.
La fréquence fondamentale d’une corde vibrante est inversement proportionnelle à sa longueur et à sa masse par unité de longueur, et proportionnelle à la tension qui lui est appliquée. Les cordes graves du piano ont un diamètre plus grand et sont plus longues que les cordes aiguës.
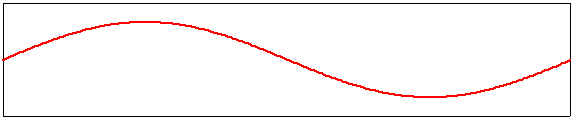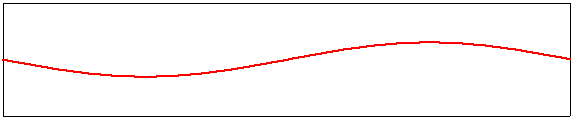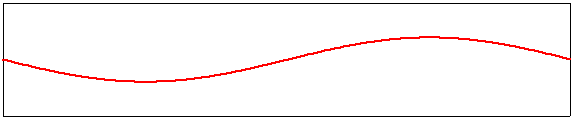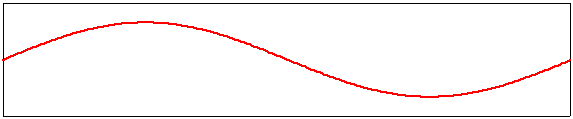
Corde vibrante : les harmoniques
L’image ci-dessus illustre les autres modes de vibration possibles des cordes vibrantes. Le mode 2 fait apparaître un point milieu et deux arcs de part et d’autre . Le point immobile est appelé un noeud, les sommets des arcs sont appelés des ventres. La fréquence du mode 2 est le double de la fondamentale. Une corde peut donc vibrer de façon complexe selon plusieurs modes simultanés, chaque mode de vibration faisant apparaître une fréquence multiple de la fréquence fondamentale.Les musicien le savent qui posent un doigt sur la corde à l’endroit d’un noeud ou d’un ventre pour mettre en évidence les harmoniques sélectionnés.
La physique nous a montré grâce à Joseph Fourier (1768-1830) que toute fonction périodique de fréquence F0 (fréquence fondamentale) peut être décomposée en une somme de signaux sinusoïdaux (les harmoniques) dont les fréquences sont les multiples entiers de F0 (2F0 3F0 … nF0).




